Преди време ви запознахме повърхностно с основните принципи във физиката, които карат самолетите да летят. Днес ще хвърлим малко повече светлината върху математическите аспекти около този проблем за тези от вас, които искат да се задълбочат. Аеродинамиката е сложна материя, но тук ще се постараем да я представим на разбираем език, синтезирайки най-важното от дебелите учебници в няколко страници.
Координатни системи
Аеродинамиката, подобно на всеки дял от физиката, разглежда сили на взаимодействие между (материални) обекти. В случая – на въздушната среда с летателния апарат. И тъй като се занимаваме със сили, т.е. някакви вектори, трябва да въведем и координатна система, преди да ги опишем математически. Координатната система е нещо напълно условно, тя е просто една отправна рамка.
Няма никакъв проблем да опишем силите, действащи върху самолет, в координатна система с център Слънцето. Крайните резултати, които ще получим при решението на динамичните уравнения, ще са същите, както при всяка друга координатна система, неподвижна спрямо самолета или намираща се в състояние на равномерно праволинейно движение. Правим това досадно отклонение, защото то е един от фундаменталните принципи във физиката – т.нар. принцип на относителността, предложен от Галилей и доразвит от Айнщайн. Правим го, и защото така може би ще е по-лесно да схванете изобилието от координатни системи, използвани в аеродинамиката и навигацията, за да изразят едно и също нещо, но отнесено спрямо летателния апарат, въздуха или земята.
Идеята не е да си усложняваме живота с изобилие от координатни системи, а да изберем такава координатна система, че уравненията, които ще получим да са максимално прости. И тъй като аеродинамиката се занимава със силите, действащи на летателен апарат, съвсем логично е за начало на координатната система да се вземе центъра му на тежестта. Следващата стъпка е да насочим оста Х в някаква посока от пространството. Тук работите почват да стават малко объркани.
Ето защо. Нека си представим един самолет в полет. Вземайки под внимание симетрията на неговата геометрична форма, ние бихме могли да построим оста Х, прекарвайки я от центъра на тежестта към носа на самолета. Но това е само единият вариант. В общия случай векторът на скоростта на самолета не съвпада по посока с геометричната му ос Х, а пък ние може да искаме нашата ос Х да е насочена именно по посока скоростта на самолета. Кой от двата варианта да изберем? Ами, и двата! В аеродинамиката първият случай е известен като свързана координатна система OXYZ, а вторият случай като скоростна координатна система ОХaУaZa. В англоезичната литература те са известни съответно като body frame и wind frame.
- Свързана координатна система
При свързаната координатна система оста, насочена по дължината на самолета в равнината на симетрия, по посока, съвпадаща с погледа на пилота, се нарича надлъжна ос и се бележи с Х. Насочена нагоре е нормалната ос У, а перпендикулярно на тези две оси и насочена по дясната част на крилото (дясното полукрило) е напречната ос Z.
Ъгълът ϑ между надлъжната ос на самолета и хоризонтална равнина се нарича ъгъл на тангаж или просто тангаж. При положителни стойности на тангажа носът на самолета е насочен нагоре спрямо хоризонта и се казва, че самолетът кабрира; при отрицателен тангаж носът на самолета е насочен надолу спрямо хоризонта и се казва, че самолетът пикира.
Ъгълът ѱ между вертикална спрямо земната повърхност равнина и проекцията на надлъжната ос в хоризонтална равнина се нарича ъгъл на рискание. Ако ориентираме вертикалната равнина в посока север-юг, то ъгълът на рискание дава информация за курса на самолета и се нарича още курсов ъгъл или просто курс (както е по-широко известен).
Ъгълът γ определя завъртането на самолета около надлъжната му ос и се нарича ъгъл на напречен наклон (крен). Курсът, тангажът и кренът са трите параметъра, които напълно определят пространственото движение на самолета.
В англоезичната литература тангажът се нарича pitch, курсът – yaw, а кренът – roll. Осите също са по-различно разположени спрямо стандарта, използван в България и страните от бившия Източен блок. Оста Х съвпада, но оста Z e насочена по вертикала надолу, а оста Y – по дясното полукрило.
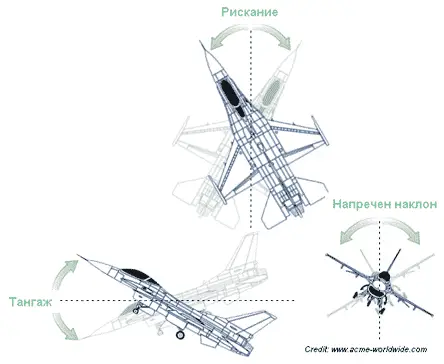
Изображение на ъглите на тангаж, рискание (курс) и напречен наклон (крен).
- Скоростна координатна система
Скоростната координатна система е по-слабо известна от свързаната и донякъде използването й е по-застъпено в теоретичните трудове, отколкото в практиката. При нея ОХа се нарича скоростна ос и е насочена по посока на вектора на скоростта на самолета. В равнината на симетрия, насочена нагоре и перпендикулярна на скоростната ос е оста ОУа , наречена ос на подемната сила. Перпендикулярна на тези две оси и насочена по дясното полукрило е напречната ос ОZа.
Както вече казахме, направленията на осите на скоростната и свързаната координатна система може да съвпадат, но в общия случай не съвпадат. Ако оста ОХа се проектира в равнината ОХУ на свързаната координатна система, ъгълът α между проекцията на ОХа и оста ОХ се нарича ъгъл на атака (на английски – angle of attack). Той е положителен, ако самолетът среща въздушния поток с долната си повърхност. Ъгълът β, който се получава между равнината ОХУ и оста ОХа е известен като ъгъл на плъзгане (на английски – angle of sideslip).Той е положителен, ако се плъзга дясното полукрило – т.е. носът на самолета се отклонява на ляво.
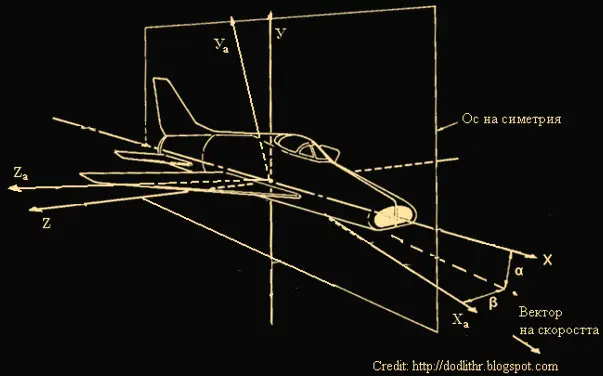
Ъгли на атака и плъзгане в скоростната координатна система.
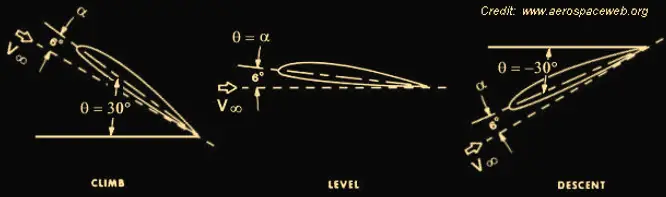
Ако се питате какъв е смисълът от тази скоростна координатна система, ето обяснението. Докато в свързаната координатна система тангажът, кренът и курсът ни показват положението на самолета в пространството, то ъглите на атака и плъзгане ни показват положението на самолета спрямо насрещния въздушен поток. Тоест, от тях зависят кинематичните параметри на полета – сили и моменти, действащи на самолета. На практика много често ъгълът на атака бива бъркан с тангажа, а ъгълът на плъзгане – с рисканието (курса). Те обаче са напълно независими. За илюстрация на това може да послужи долната картинка, на която е показан профила на крило с положителна кривина в три различни случая: при ϑ = 300, ϑ = 60 и ϑ = -300. Ъгълът на атака обаче е един и същ и в трите случая α = 60.
Аеродинамична сила
Щом като вече се запознахме с координатните системи, може да започнем да въвеждаме и аеродинамичните сили. По-коректно, това е една-единствена сила, получаваща се при обтичането на летателният апарат от въздуха. Тя се свежда до един вектор, който е равнодействащата на всички сили на триене и сили от налягане, възникващи при обтичането. Тази пълна аеродинамична сила Ra е приложена в точка, известна като център на налягането. С увеличаването на скоростта и ъгъла на атака векторът на тя променя големината и посоката си и затова разглеждането й при теоретичните зависимости не е удобно.
Поради тази причина за удобство и напълно условно аеродинамичната сила се разглежда като две отделни сили. И тъй, проекциите на пълната аеродинамична сила в скоростната к.с. са подемната сила Ya и силата на челно съпротивление Ха.
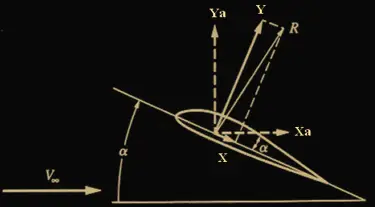
Основната задача на аеродинамиката е да установи как се изменят Ya и Ха като функция на различни параметри – скорост, ъгъл на атака, плътност на въздуха и др.
Подемна сила
Подемната сила носи самолета във въздуха и затова силно ни вълнува характерът на изменението й при промяната на различни променливи. Всъщност формулата, която я описва количествено, изглежда подозрително просто:
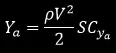
Тук ρ е плътността на въздуха, в който летим, V е скоростта на обтичане на въздушния поток (скоростта, с която се движим), S е характерна площ (в случай, че разглеждаме само крилото, което създава повечето подемна сила, за удобство е прието да изберем неговата площ в план), a CYa e поправъчен коефициент на подемната сила (в англоезичната литература CL). Именно с тоя коефициент започват главоболията. Така че ако искаме да сметнем пълната подемната сила на един самолет, простата формула отгоре с подробно разписаното аналитично определение за CYa (където ги има) ще набъбне застрашително.
- Изменение на коефициента на подемната сила в зависимост от ъгъла на атака
Но все пак нещата не са толкова страшни. На първо място трябва да споменем, че коефициентът CYa в най-голяма степен зависи от ъгъла на атака на профила на крилото по следната проста зависимост:
![]()
Тук ![]() е производната на коефициента на подемна сила. Това пак е коефициент, чиято стойност показва наклона на зависимостта (а тя, би трябвало да се досетите от уравнението, е права линия). Ъгълът на атака е α, а α0 е ъгълът на атака при нулева подемна сила – т.е. този ъгъл на атака, при който не се създава подемна сила (отрицателен за повечето профили на крилото и нулев за симетричните).
е производната на коефициента на подемна сила. Това пак е коефициент, чиято стойност показва наклона на зависимостта (а тя, би трябвало да се досетите от уравнението, е права линия). Ъгълът на атака е α, а α0 е ъгълът на атака при нулева подемна сила – т.е. този ъгъл на атака, при който не се създава подемна сила (отрицателен за повечето профили на крилото и нулев за симетричните).
С други думи, увеличавайки ъгъла на атака, ние увеличаваме и подемната сила. Това е причината самолетите да излитат със спуснати задкрилки при излитане – спуснатата механизация на крилото де факто увеличава ъгъла му на атака и от тук увеличава и подемната му сила (около 3-4 пъти), така че става възможно по-бързо излитане при сравнително ниски скорости на засилване. Големите самолети въобще не биха могли да излетят от съвременните летища, без да се прибягва до този прийом.
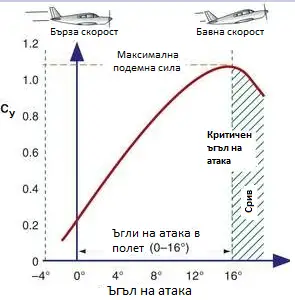
Това свойство е много удобно, защото позволява да се лети при ниски скорости, които могат да се създадат от прости и евтини двигатели. Но има едно „но“… Не можем да увеличаваме ъгъла на атака безкрайно. Още при 10-150 въздушният поток над крилото започва да се „откъсва” – обтичането му вече не е плавно, появяват се турбулентни завихряния, които рязко намаляват подемната сила. Ъгълът на атака, при който започва да се случва това, се нарича ъгъл на начално откъсване.

Формиране на турбулентни завихряния при увеличаване ъгъл на атака. Изображение: aviation-history.com
Ако продължим да увеличаваме ъгъла на атака и нататък, подемната сила продължава да расте, но вече нелинейно. Стига се до максимум на подемната сила при ъгъл на атака, наречен критичен ъгъл на атака. Сетне се случва нещо крайно неприятно. При още по-голям ъгъл на атака подемната сила намалява рязко и значително – явление, наречено срив на потока. От сривен режим на полет самолетите трудно се измъкват и обикновено той завършва с катастрофа. Сривът на потока е най-голямата опасност за летците и въпреки че всички пилоти са наясно с това, огромен брой катастрофи са причинени именно поради допускане и задълбочаване на сривен режим. На долното видео можете да видите Boeing 747-800 в сривен режим на полет като част от полетните тестове, провеждани при допускане в експлоатация.
Tъй като завихрянията по крилото, съпровождащи срива, се формират хаотично, пилотът усеща, че самолетът започва да се тресе (явление, наречено бафтинг). Инстинктивната му реакция в този случай е да дръпне щурвала към себе си, за да предотврати падането на самолета. Но така той само задълбочава срива и подемната сила намалява още повече. Обтичането на крилото става твърде несиметрично и самолетът навлиза в неуправляемо състояние, наричано свредел. Изходът от свредел е най-вероятно катастрофален, защото е много трудно посредством управляващите си въздействия пилотът да върне самолета от неустановен в установен режим на полет.
- Изменение на коефициента на подемната сила в зависимост от скоростта на полета
Друга важна зависимост е промяната на коефициента CYa при промяна на скоростта. Ако се върнем на формулата, по която се изчислява подемната сила, бихме могли да заключим, че коефициентът на подемната сила се увеличава квадратично с нарастването на скоростта. Но всъщност той следва доста по-сложна зависимост, която отчита вискозността и свиваемостта на въздуха, както и геометрията на самото крило. Графично тази зависимост изглежда принципно така:
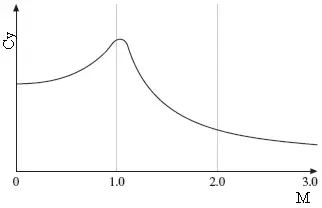
Тук по Х е нанесена скоростта на звука, изразена чрез числото на Мах (М). Както виждате при ниски скорости (до около 0,5 M) квадратичната зависимост е налице, но след това темпът на нарастване намалява, а при свръхзвуково обтичане (М > 1) картината драматично се променя и коефициентът на подемна сила всъщност започва стремглаво да намалява в началото, а още по-нататък се стабилизира.
И също както имаме критичен ъгъл на атака, след който настъпва срив на потока, така имаме и минимална скорост на летене, под която също настъпва срив. Но за разлика от критичния ъгъл на атака, който зависи единствено от параметрите на крилото (геометрия, форма на профила), то сривната скорост се влияе от редица фактори. Сред тях са теглото на самолета, ъгъла на напречен наклон, ъгъла на атака, височината и съответно плътността на въздуха. Любопитна подробност е, че заради намаляващата плътност с увеличаване на височината сривната скорост непрекъснато се увеличава и на някаква височина тя става равна на максималната скорост, която може да достигне самолетът. При това положение подемната сила, създавана от самолета, е равна на силата на теглото му и той не може да набира повече височина.
Тази височина се нарича статичен таван и за повечето съвременни пътнически самолети е около 12 500 m. С подходяща геометрия и голямо крило обаче е възможно да се достигнат и по-големи височини – прословутият U2 на USAF e можел да се издига до 21 000 m.
- Изменение на коефициента на подемната сила в зависимост от геометричните параметри на крилото
Основната част от подемната сила на самолет се създава от крилото, така че неговата форма има огромно значение за големината на коефициента на подемната сила. Нещо повече – различната форма на крилото променя коренно зависимостите, които разгледахме по-горе. И като говорим за различна форма, имаме предвид две неща – формата на профила на крилото и формата на крилото в план.
Дизайнът им зависи от целите, за които е конструиран самолетът. Поради това формата на профила може да бъде много разнообразна – несиметрична (при което се създава подемна сила и при нулев ъгъл на атака) и симетрична (подходящо решение за акробатични самолети). Драстична е разликата между профилите за дозвукови полети и тези за свръхзвукови. Последните са много тънки и с остър атакуващ ръб, чрез което се избягва образуването на отсъединен челен скок на уплътнение в свръхзвуковия поток и се намаляват загубите от съпротивлението. По-долу са дадени за сравнение различни видове профили:

Принципно профилите с голяма кривина и дебелина създават повече подемна сила при по-малки ъгли на атака спрямо профилите с малка кривина и дебелина. Графично нещата изглеждат така:
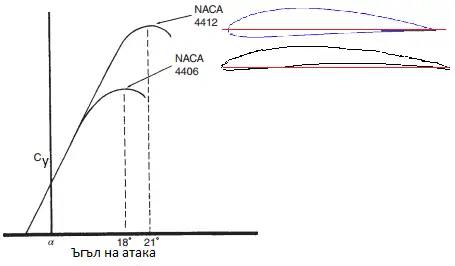
Влияние на дебелината на профила върху коефициента на подемна сила. Изображение: Flight Theory and Aerodynamics – A Practical Guide for Operational Safety
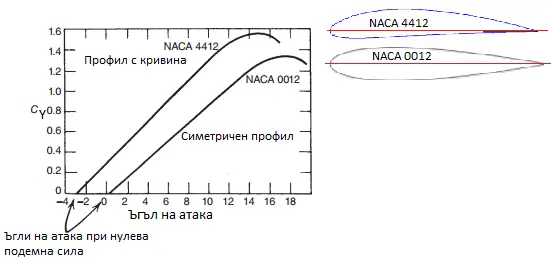
Влияние на кривината на профила върху коефициента на подемна сила. Изображение: Flight Theory and Aerodynamics – A Practical Guide for Operational Safety
Причината за увеличението на коефициента е, че поради по-голямата кривина и дебелина, въздушният поток върху горната повърхност на крилото се ускорява до по-високи скорости. Това увеличава разликата в наляганията между горната и долната повърхност заради ефекта на Бернули и така увеличава подемната сила на крилото. Но както ще видим по-нататък, подобни профили увеличават съществено и силата на челно съпротивление, което ги прави непредпочитани в съвременната авиация.
Що се отнася до геометрията на крилото в план, там вариантите са концептуално пет – право, трапецовидно, елипсовидно, стреловидно и триъгълно крило.
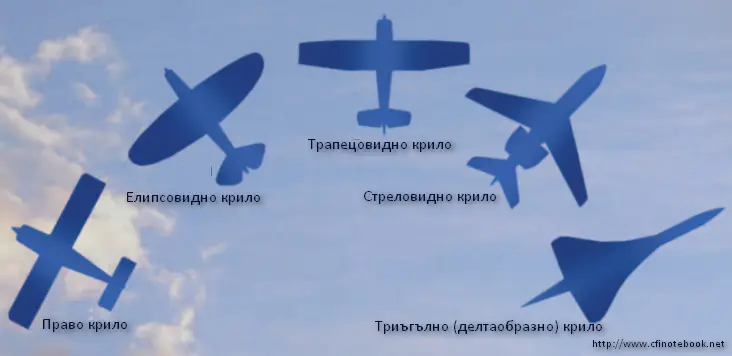
На база на тези основни типове съществуват най-разнообразни варианти, а също така има и крила, които променят геометрията си в план, според скоростта на полет. Тази особеност подсказва, че ако крило с някаква форма е максимално ефективно при дадена скорост, то при друга скорост най-голяма ефективност се постига при друга форма на крилото. Освен това различната форма на крилото в план влияе силно и на зависимостта от ъгъла на атака. Справка – тази графика:
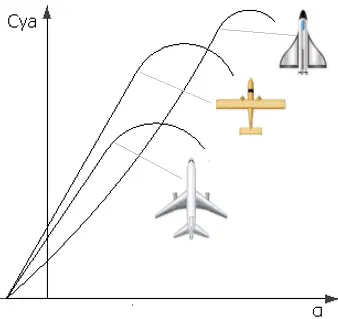
Както виждате, абсолютен шампион е триъгълното крило. При него потокът се откъсва още на предния ръб и се турбулизира, което пък води до задържането му в останалата част на крилото и способства достигането на критични ъгли на атака до 30 – 40 градуса. Най-зле тук се представя стреловидното крило. To е най-натоварено в крайните си сечения, които са и най-податливи към ранно откъсване на потока. А това обяснява защо този вид крило има най-малък критичен ъгъл на атака. Което пък от своя страна е много неприятно. И понеже стреловидното крило е абсолютен хегемон в дизайна на съвременните пътнически самолети интерес поражда въпросът как проектантите са се преборили с тоя проблем. Основно по два начина:
- Чрез „усукване“ на крилото. Т.е. профилите в крайните сечения имат по-малък ъгъл на поставяне спрямо профилите в основните сечения, така че техният действителен ъгъл на атака също е по-малък;
- Чрез поставяне на генератори на вихри по горната повърхност на крилото. Ако по време на полет сте седели на място до прозорците около крилото, много вероятно е да сте се питали какви са тези странни стърчащи ламаринки по повърхността. Е, на път сте да узнаете каква е тяхната функция. Както показва името им, те спомагат за завихрянето на потока по горната повърхност на крилото. Така обтичането става от ламинарно на турбулентно, а турбулентният поток има хубавото свойство да се откъсва при големи ъгли на атака.

Генератори на вихри по крилото на Boeing 737-800. Снимка: Bill Abbott
Що се отнася до графичната зависимост на коефициента на подемна сила от скоростта (числото М) за трите основни типа крило (право, стреловидно и триъгълно), тя изглежда така:
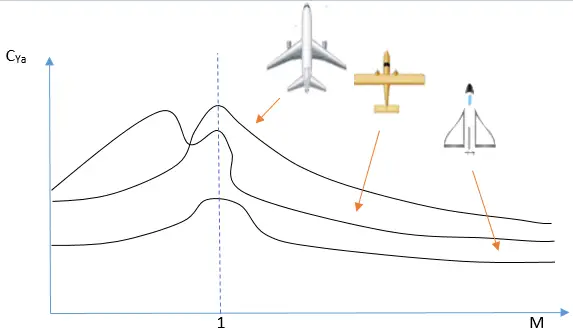
Защо изглежда така, не можем да обясним с няколко изречения. Има причина учебниците по аеродинамика да са дебели тухли. Важното в случая е, че при ниски скорости правото крило създава най-много подемна сила спрямо останалите типове, докато в свръхзвуковия диапазон и трите типа създават горе-долу равна подемна сила.
- Влияние на земята върху подемната сила (екраниращ ефект)
Близостта до земната повърхност също води до промяна на подемната сила. Това влияние, наречено екраниращ ефект, се появява на височина, равна на разпереността на самолета или диаметъра на носещия винт на вертолет, и се усилва с намаляването й. Ето какво се с случва. Колкото по-малко е разстоянието между крилото и земята, толкова повече нараства налягането на въздуха върху долната повърхност на крилото. Това води и до по-интензивно протичане на въздух през предния ръб на крилото. Което пък ускорява въздушния поток по горната повърхност и там налягането намалява. Нетният ефект от всичко това е допълнителна подемна сила.

Хеликоптер на US Navy, създаващ екраниращ ефект над водната повърхност. Изтласкваният надолу въздух от носещия винт се отклонява от водната повърхност, което води до сила на реакция у хеликоптера, насочена нагоре. Третият закон на Нютон в действие. Снимка: US Navy / Sarah E. Ard
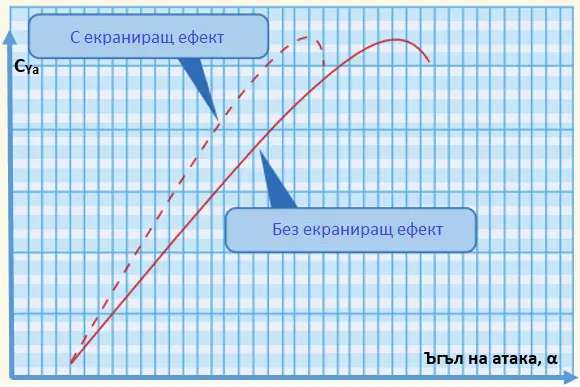
Влияние на земната повърхност върху коефициента на подемна сила в зависимост от ъгъла на атака
E, ами това беше за подемната сила. Следващият път ще погледнем другата страна на монетата и ще разкажем нещичко и за челното съпротивление.
Използвана литература:
Аеродинамика на летателните апарати, Диан Гешев, 2001, ТУ София
Още материали за аеродинамиката:
Динамика на полета – аеродинамични моменти
Въздушно съпротивление в аеродинамиката
Основи на аеродинамиката или защо летят самолетите

