“It’s not rocket science” е стандартният израз, когато англоезичните искат да кажат, че нещо си е лесно. За разлика от науката за ракетите, която явно не е. Дали това е вярно ще прецените сами, прочитайки първата от поредицата ни публикации, в които ще ви запознаваме с основните принципи, използвани при конструирането на ракети.
- Вместо въведение
Като цяло ракетите се подчиняват на изключително прости правила, както във физиката на задвижването си, така и в своята конструкция. Обаче високите изисквания, които често се поставят пред тях, водят до това, че трябва да се отчитат множество наглед дребни детайли. И благодарение на тях нашата първоначално проста ракета неусетно се превръща в една доста сложна система. Но е добре винаги да си спомняме, че в същността си ракетите са нещо много просто. За разлика от да речем автомобилите или компютрите, които по принцип са си сложни.
- Малко физика
Да започнем от тук: кое прави ракетата ракета; кое я кара да се движи? За да си отговорим на този въпрос, ще трябва да се върнем към това, което сме научили в 6-ти клас по предмета, сега наричащ се „Човекът и природата”, а по мое време Природознание. Та там за първи път ни се споменават едни неща, наречени Трите принципа на механиката. Ще оставя на вас да си преговорите първите два принципа, но ще се спра на третия, тъй като той е много важен за ракетите. И така, Третият принцип на механиката гласеше, че:
„Ако едно тяло, въздейства на друго тяло с дадена сила, то второто тяло му
противодейства с равна по големина и противоположна по посока сила”.
Наглед това звучи разбираемо, но далеч не е очевидно. Представете си например един пирон и един чук, с който забивате пирона в дъска. В ежедневието си казваме, че на пирона прилагаме сила чрез чука и заради тази сила пиронът се забива навътре в дъската. Но това е само половината от картинката. Ние като че ли не забелязваме факта, че всеки път, когато удряме пирона, той ни отвръща със същата сила, насочена към нас (ако това не беше вярно, чукът щеше да минава през пирона, все едно го няма). А не го забелязваме, защото не ни интересува – в случая е важна тази сила, която кара пирона да се забива. Другата сила (да я наречем реакция), е без значение за заковаването на пирона.
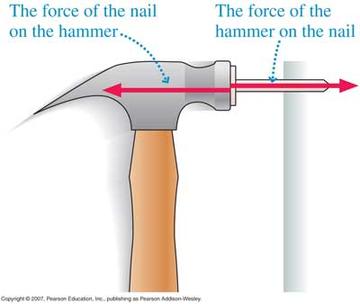
При ракетата имаме аналогична ситуация – действа й сила, която съответно създава у ракетата равна по големина и обратна по посока реакция. Само че за разлика от коването на пирони, в този случай нас ни интересува реакцията, защото тъкмо заради нея ракетата се движи. Затова и на движението на ракетите му викат реактивно движение.
Най-общо ние можем да оприличим ракетите на куха тръба, чийто един край е затворен, а вътрешността на тръбата е запълнена с горим материал. Когато горивото започне да изгаря, продуктите на изгарянето напускат тръбата през отворения й край. Тези продукти са някакви газове, съставени от молекули, които естествено притежават маса, а освен това заради изгарянето се ускоряват до някаква скорост, с която напускат тръбата. Така че имаме маса, имаме и ускорение => следователно имаме и сила. Както виждате от картинката долу, тази сила (F) e насочена надолу, по посока на изтичащите газове. Насочена е така, защото силата F определя движението на молекулите на газа, които излизат от ракетата. А излизайки от ракетата, газовите молекули създават реакция R в самата ракета, равна на силата, с която изтичат, но с обратна посока. Това, както току-що разбрахме (си припомнихме), е необходимо, за да се спази Третия принцип на механиката. И тази реакция е причината, заради която ракетата се издига нагоре.

Изображение: Steve Jurvetson
- Малко сметки
Дотук би трябвало да ни се е изяснило какво кара ракетите да се движат от физическа гледна точка, но все още сме далеч от количественето описание на движението, което би ни вълнувало, ако бяхме ракетни инженери. Е, нека бъдем! Поне за пет минути. Долу съм описал някои базисни сметки, касаещи ракетите, колкото се може по-подробно.Ако сте на ти с физиката или ако тя ви отегчава, можете да се прехвърлите направо на следващата точка.
И така, имаме две равни по големина сили F и R с противоположна посока. Силата F можем да открием, като умножим сбора на масите на всички изтичащи молекули (mi) по ускорението, което имат, променяйки скоростта си от 0 m/s във вътрешността на ракетата до крайната скорост u на изхода на ракетата (втори принцип на механиката – силата е масата по ускорението). Аналогично – реакцията R, заради която ракетата се движи, е равна на масата на ракетата M по нейното ускорение. Тоест:
Тук сме използвали, че ускорението е равно на скоростта, разделена на времето, а с ∆-символите искаме да кажем, че разглеждаме достатъчно малко изменение на скоростта, за което то е постоянно във времето. Страхотно, но имаме лек проблем – в това уравнение използваме величини, чиято стойност ни е неизвестна и следователно уравнението в този си вид не ни върши никаква работа. Ние знаем само:
– масовият разход на гориво – ∆М / ∆t, измерващ се в kg/s. Той ни показва изхвърленото от ракетата вещество за единица време, което също така е равно на олекването на самата ракетата;
– скоростта u, която имат газовете на изхода на ракетата.
Трябва да вкараме някак си тези две величини в горното равенство. Мога веднага да ви напиша резултата, той изглежда почти идентично, но начинът, по който се стига до него всъщност далеч не е толкова очевиден, колкото бихте си помислили. Така че пригответе се да минем през още малко фундаментална физика…
Там, във физиката, често се използва една величина, наречена импулс. Импулсът показва количествено действието на постоянна сила във времето: p = F*t. А тъй като F = m*a = m*(v / t), това означава, че импулсът е просто масата на обекта, върху който действа силата, по неговата скорост: p = m*v. Ако разглеждаме сила и нейното противодействие във времето, е по-удачно да боравим с техните импулси и по аналогия както F = -R, така и p1 = -p2. Или ако поразместим малко: p1+p2 = 0. Вгледайте се хубаво в това равенство, защото то е сред най-важните в цялата физика – сборът на двата импулса никога не се променя. Ако едно тяло, което се движи с някаква скорост се сблъска с друго тяло с друга скорост, то скоростите им след сблъсъка ще се променят, но не и сборът от импулсите им. Нарича се закон за запазване на импулсите и важи с пълна сила и за нашата ракета.
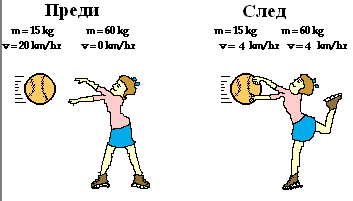
Топката притежава начален импулс, който се запазва и след като кънкьорката я хваща. Тъй като общата им маса се увеличава, за да се запази импулсът, трябва скоростта им да намалее. Изображение: physicsclassroom.com
В първия момент от време ракетата не се движи, т.е. началният й импулс е p = 0. В следващия момент обаче масата на ракетата е намаляла и тя е набрала скорост. Т.е. новият й импулс е: p1 = (M – ∆М)*∆V, където М е началната й маса, ∆М е намаляването на масата й, а ∆V – нарастването на скоростта й. Същевременно изгорелите газове, които се изхвърлят от ракетата, също имат импулс: p2 = ∆М*(-u), където u е скоростта на газовите частици спрямо неподвижната земя (минусът е, защото те се движат обратно на ракетата) . Сборът на тези импулси не се променя и в случая е равен на нула:
0 = p1 + p2
0 = (M – ∆М)*∆V + ∆М*(-u)
0 = M*∆V – ∆М*∆V – ∆М*(-u).
Членът „∆М*∆V” в това равенство можем да пренебрегнем, тъй като Δ-символът показва, че работим с много малки величини, които умножени една с друга стават още по-малки в сравнение с другите членове на уравнението. В края на краищата получаваме: M*∆V= ∆М*u, което изразено чрез сили (делим двете страни на време) е:
Ура! Най-сетне имаме уравнение, което описва движението на ракетата с известни нам величини. (∆М / ∆t)*u – това е теглителната сила на ракетата, а (∆V / ∆t)*M – това е реактивната сила на ракетата, даваща ни нейното ускорение, от което можем да изразим скоростта и траекторията й.
И как ще намерим скоростта на ракетата, да речем 10 минути, след като сме я изстреляли? Оказва се, че математиката ни позволява доста бързо да се справим с тази задача. Съществува операция, чрез която можем да намерим сумата от нарастванията на скоростта (сумата от ∆V ) в даден момент от времето (сума от ∆t). Тази операция се нарича интегриране. Интегрирането не е особено интуитивно и изисква сравнително добри математически познания, така че аз само ще си позволя да покажа крайния отговор, който се получава, след като приложим тази загадъчна операция на уравнението ни.
- Уравнение на Циолковски
Това е крайъгълният камък на цялата наука за ракетите.
Нарича се уравнение на Циолковски, на името на руския учен Константин Циолковски, който пръв е стигнал до него в началото на 20-ти век. Тук u е скоростта на изтичащите газове от ракетата, m e началната маса на ракетата, m1 e масата на ракетата в някакъв момент от време, а V е скоростта й в същия момент от време („ln”, ако се чудите, обозначава операцията логаритмуване).

Уравнението на Циолковски описва движението както на най-голямата ракета, построявана някога – Saturn V…

… така и на ракетите-играчки като този умален модел на Saturn V.
Това стегнато уравнение ни казва много за ракетите. На първо място е видно, че скоростта на ракетата ще нараства непрекъснато с времето, докато все още има гориво за изгаряне. Тази скорост V ще е толкова по-голяма, колкото е по-голяма разликата между началната и текущата маса (съотношението m/m1) и колкото е по-голяма скоростта на изтичане на газовете.
От тук можем да намерим и максималната скорост на ракетата. Тъй като стойността на u остава постоянна величина през полета на ракетата (в най-простия случай), то това на практика означава, че максималната скорост на ракетата ще се определя от отношението на началната към крайната й маса: m/mкр. Това съотношение (на английски mass ratio) e eдин от важните параметри в ракетното инженерство, показващ ефективността на ракетата. Колкото по-голямо е съотношението на масите, толкова по-бърза е ракетата, но и толкова повече от масата на ракетата се пада на горивото. Така че за да бъде възможно най-бърза ракетата, тя трябва да съдържа колкото се може повече гориво, за сметка на теглото на празната ракета. Ако съотношението на масите е по-голямо от 2,718, (при това съотношение стойността на логаритъма е единица) скоростта на ракетата в някакъв момент става по-голяма от скоростта на изтичане на газовете.
Максималната скорост на ракетата определя и максиималната далечина на полета й. Така например за една балистична ракета с обсег 100 km e достатъчно m/mкр да е около 1,5, а ако обсегът е 1200 km, то m/mкр се увеличава на 4, т.е. 75% от масата на ракетата е гориво. Изглежда логично обсегът на ракетите да нараства, като се увеличава съотношението на масите. Но този параметър не може да расте непрекъснато – практически е невъзможно да се построи едностепенна ракета със съотношение на масите по-голямо от 10.
Другият параметър в уравнението на Циолковски, показващ ефективността на ракетите, е скоростта на изходящите газове u (еffective exhaust velocity). Първите ракети, използващи за гориво барут, са имали скорост на изтичащите газове от около 2 000m/s. Най-съвременните течногоривни ракети днес могат да произведат u до 4 500 m/s, което е близо до теоретичната граница за ракета, използваща за полета си енергия от химически процес.
Скоростта на изтичане на газовете от ракетата зависи от много неща:
– от разликата между налягането на изхода на ракетата (соплото) и атмосферата. Колкото е по-голяма тази разлика, толкова повече u се увеличава, с което нараства и теглителната сила на ракетата. Във вакуум (космоса) няма атмосфера и разликата е максимална, u е най-голямо по стойност, а ракетата – най-ефективна;
– от конструкцията на соплото;
– от молекулярното тегло на горивото – колкото по-малко е това тегло, толкова скоростта u е по-висока. Следователно, колкото по-леко гориво използваме, толкова по-добре. Ползата от това е толкова значителна, че в някои ракети, използващи течен водород за гориво и течен кислород за окислител, се добавя допълнителен водород, който не участва в горенето, само и само за да се намали молекулярното тегло на изхвърляните газове.
– от температурата на изгаряне на горивото – колкото по-висока е тя, толкова по-бързо газовете ще излизат от ракетата.
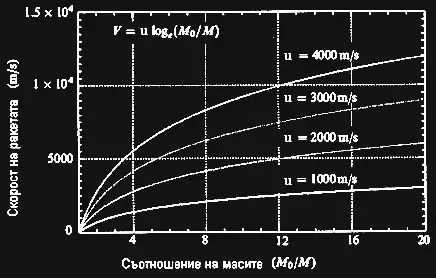
Тази графика ни показва крайна скорост на ракетата в зависимост от съотношението на масите и скоростта на изходящите газове. Изображение: Rocket and spacecraft propulsion: principles, practice and new developments (3th edition)
В практиката обаче рядко се говори за скоростта на изходящите газове. Вместо нея е разпространено едно друго понятие, което фактически означава същото, но се нарича специфичен импулс (specific impulse). Специфичният импулс се намира като разделим изходящата скорост на газовете u на земното ускорение g: Isp = u / g. Според тази дефиниция той има размерност секунди и на пръв поглед е с неясен физичен смисъл. Може би е специфичен, но със сигурност не е импулс от гледна точка на физическата терминология. И защо тогава си усложняваме живота с него? Ами защото традицията така повелява (голям аргумент!) и заради размерността му – секунда. Секундата си е секунда във всяка измервателна система, което е хубаво, защото по принцип ракетното инженерство е ожесточена арена на сблъсъка между имперската мерна система и метрична мерна система. А историята помни не един и два идиотски провала на ракети заради недоразбиране на мерните системи.
Има и още една причина да се използва специфичния импулс, при това физическа, но за жалост обяснението е твърде завъртяно и предизвиква главоболие…
Изгаряте от желание да научите, нали? Е, добре ето: излъгах ви – специфичният импулс си е и специфичен, и импулс! Официално той се дефинира като отношение на създадената за единица време теглителна сила на ракетата (нейният импулс – F*Δt) към теглото на изгаряното гориво за единица време (разходът на гориво*g* Δt) или:
![]()
Всъщност специфичният импулс дава нагледна представа за ефективността на горивото – с колкото по-голяма стойност е Isp толкова по-малко количество гориво е нужно, за да се постигне даден импулс. Реципрочната стойност на Isp е прието да се нарича специфичен разход на ракетно гориво – SPC и той показва масовия разход на гориво, необходим за произвеждането на 1 N тяга. Означава ли всичко това, че колкото по-висок специфичен импулс има една ракета, толкова по-мощна е тя? Нищо подобно – високата стойност на специфичния импулс просто намеква, че някога ракетата ще се ускори до висока скорост, но не ни казва след колко време ще стане това, т.е. може да се окаже (и най-често се оказва), че ускорението на ракета с висок специфичен импулс, а следователно и нейната теглителната й сила, е някакво мижаво число.
- Стига толкова
Това беше възможно най-най-важното, което може да се каже за ракетите, поне като за начало. Може би си мислите, че вече знаете много, или пък сте на мнение, че нищо не разбрахте? Нямам представа, но това, което споделих с вас, описва възможно най-простия модел на ракета, в който се занимаваме само с нейната реактивна сила.

В реалността картината е доста по-комплицирана. Освен реакцията от изхвърляните газове, на ракетата действат поне още две сили, които по никакъв начин не можем да пренебрегнем, ако искаме да опишем правилно полета й. Това са:
– силата на тежестта – с издигане на ракетата във височина тази сила намалява, поради намаляването на масата на ракетата и поради намаляването на земното ускорение g във височина (за малки ракети, това не е от значение, но не и за космическите);
– силата на въздушно съпротивление – тя не зависи от масата на ракетата, а от напречното й сечение. Във височина също намалява, тъй като въздухът става все по-рядък.
Да отбележим и че разходът на горивото, както и скоростта на изходящите газове, които взехме за постоянни, в най-общия случай могат да се променят по някаква зависимост. Така че изчисляването на траекторията на една ракета се оказва мъчна задача. Но колкото и сложна функция да описва движението й, вече знаете, че в основата й седи едно простичко твърдение: всяко действие има противодействие. Останалото са подробности.


Интерсно ми е,защо след старта космическите совалки се завъртат около надлъжната си ос,а просто преди това,не са поставени в „правилната“ пзиция? Благодаря!
Извинявай, Викторе, че се забавихме толкова с коментара ти, но за съжаление имахме някои технически неуредици със сайта тия дни. Иначе относно въпроса ти – завъртането на совалките около надлъжната им ос бе част от маневрата, при която те се обръщаха, образно казано, с „гърба“ си към земната повърхност. Всичко това се правеше, за да могат совалките да се насочат в необходимата орбита, която обикновено трябваше да осигури скачване с Международната космическа станция. Ориентацията на стартовите площадки, от които се изстрелваха совалките (39А и 39В) е север- юг, което означава, че ако совалките само се обръщаха по гръб, без да… Read more »
Благодаря,Емиле!
Приличам на каруцар,който иска да разбере технически подробности от булидите във Формула 1. Отговорът Ви е разбираем,но аз не мога да го „преведа“ за себе си,защото знам,че всички ракети се изстрелват от земната повърхност в источна посока.Едва след като са вече на първоначалната околоземна орбита /някъде около екватора/ ,надлъжната им ос се насочва встрани и двигателите коригират курса в нова с по-голям ъгъл спрямо екваторната плоскост орбита. Простете на каруцаря,моля,който не може да формулира добре въпроса,камо ли да разбере отговора.
Не се чувствайте длъжен да ми отговаряте повече по този въпрос.
Благодаря Ви много!
Всички сме каруцари, няма страшно 🙂 Прав си, че ракетите трябва да отиват на изток (известно ми е само едно изключение – израелската Шавит) и всъщност в отговора ми има подвеждаща информация, така че нищо чудно, че не е много ясен. След като огледах клипове на совалкови стартове и сравних разположението на совалките при старта с разположението на стартовите площадки в Google Maps, установих, че всъщност ако не се завъртят около надлъжната си ос, совалките ще отиват в посока юг. Това е предопределено от положението на сервизната кула, която се пада в посока запад спрямо лявото полукрило на совалката. Така… Read more »
Любопитството надвива чувството ми за срам,че ставам нахален.Ако не Ви затруднява,дайте ми адрес,където сам мога да прочета /на български/,как се поддъжа въртеливото движение на жироскопите,без това да ги разстройва по време на полет.Защото всички си мислим,че знаем–компас и … морето е до колене.Но в космоса,на път за луната да кажем,и слънце и звезди могат да бъдат от всяка една наша страна.
С неудобство – благодаря!
Най-доброто, което мога да препоръчам по този въпрос на български е една лекция, описваща начина на работа авиационен курсов жироскоп, в която е показано как се парират вредните моменти. Можеш да я изтеглиш от тук – https://drive.google.com/file/d/0B_aKTYiEFw2tTVBrWV9XNGhuMHM/view?pli=1
Малко тромаво е изложението, но мисля, че основните идеи се разбират. Имам и още по темата – описание на авиохоризонт, физика на жироскопа, ако имаш интерес само пиши, за да ги сканирам. И не се притеснявай – това е идеята на този сайт, да си споделяме информация.
Благодаря,благодаря, много благодаря! ЧАО!
Моля да извините лаика, но без да оспорвам каквото и да е в чудесния материал, а само като един „прост инженер” (не авио) се питам: Може ли на въпроса „КОЕ КАРА РАКЕТАТА ДА СЕ ДВИЖИ” да се отговори и така: Ракетата се движи защото по същество представлява един съд (тръба) в който по някакъв начин се поддържа някакво налягане и отвор от който се „губи” налягане. Или все едно имаме едно тяло (може и сфера), на което по цялата вътрешната повърхност, с изключение на липсващата площ на отвора-сопло, действат сили породени от налягането и съответно се появява неуравновесена от нищо… Read more »
Здравей, благодарим за добрите думи и коментара! Като цяло картинката, която обрисуваш в коментара си, е вярна, но изводите, до които стигаш не са съвсем точни. Действително може би е по-просто да се разгледа ракетата от гледна точка на наляганията – статично (вътре в нея) и динамично (на изходящата газова струя). Аз съм разгледал сили в материала по-горе, защото така е по-лесно да изведа уравнението на Циолковски. Но и в случая с наляганията пак ще се стигне до същата формула. Ще се опитам да го обясня нематематично.Скоростта на изтичащия газ, излизащ през отвора с по-голяма площ е по-малка от тази… Read more »
Здравейте, благодаря за бързата реакция – отговор на моя коментар. Както сте разбрали от последния, моя поглед върху ракетите както и познанията ми са съвсем любителски. Същевременно считам че не сте разбрали същността на коментара ми – в него аз не оспорвам нищо и никъде не говоря за най-ефективно използване на горивото, далечина, скорост на полета и др.п. Правя само констатацията, че е възможно да се получат еднакви теглителни (задвижващи ракетата) сили варирайки със създаваното в горивната камера налягане и отвора на соплото (и естествено с масовия разход на гориво). Ще кажете: кому е нужно това? Честно казано не знам… Read more »
Първо – моите познания по въпроса също са близо до любителските (това, което знам за ракетите, го знам от самообразоване) и също не се считам за някакъв капацитет. Второ – действително не съм разбрал същината на въпроса. Аз разглеждах случай, в който имаме две еднакви ракети, в чиито горивни камери има едно и също статично налягане. В този случай тягата на ракетата с по-малък изходящ отвор е по-голяма от тягата на ракетата с голям отвор. Ако обаче можеш да манипулираш налягането в горивната камера и масовия разход, то действително е възможно да се получат равни теглителни сили на двете ракети.… Read more »