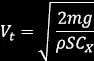Въздушно съпротивление в аеродинамиката

След като миналия път очертахме характеристиките на подемната сила в аеродинамиката, сега ще ви запознаем и с обратната страна на монетата – въздушното съпротивление. Ако сте чели и останалите материали в блога ни, посветени на аеродинамиката, вероятно си спомняте, че при обтичане на обект с въздух се получава аеродинамична сила, чийто вектор е насочен по осите Х_А и Y_А на т.нар. скоростна координатна система на обекта. Проекцията на вектора на тази сила по оста Y_А нарекохме подемна сила, а проекцията по оста Х_А сила на челно съпротивление или просто въздушно съпротивление (на английски – drag).

Практически челното съпротивление е вредната част от аеродинамичната сила.  Ако подемната сила кара летателния апарат да се издига нагоре, то челното съпротивление убива скоростта му. Така то пречи  на апарата да създаде голяма подемна сила, тъй като за голяма подемна сила ни трябва и голяма скорост. И за да компенсира челното съпротивление, нашият летателен апарат трябва да произвежда повече тяга, което увеличава разхода на гориво, което пък не е икономично.

А тъй като една от  основните цели на авиацията е да се лети максимално икономично, то борбата със съпротивлението съществува още от зараждането на всички видове въздушен транспорт. Намаляването на коефициента на челно съпротивление дори с една десетохилядна част (тази част в аеродинамиката се нарича единица съпротивление) би увеличило приходите на авиокомпаниите с милиони долари.

Но за да намалим влиянието на челното съпротивление, доколкото е възможно, преди всичко трябва да го опознаем добре. Защо има съпротивление? Какво точно представлява? От какво зависи и как се изменя? Наглед прости въпроси, които обаче водят директно към чудния свят на механиката на флуидите.

Физика на въздушното съпротивление

Формулата, от която зависи силата на въздушното съпротивление, прилича страшно много на формулата, по която се пресмята и подемната сила:

Да припомним – тук ρ е плътността на обтичащия въздух, V е скоростта на обтичане на въздушния поток (скоростта, с която се движим), S е площта на крилото в план (или друга характерна площ, ако разглеждаме произволен обект),  a C_Xa e поправъчен коефициент на въздушното съпротивление (в англоезичната литература C_D).

Подобието на формулите за подемна сила и съпротивление никак не е странно, ако вземем под внимание факта, че двете сили са условно разделени части на едно и също нещо. При това на пръв поглед може да ни се стори, че силата на въздушно съпротивление се влияе от същите фактори като подемната сила. Т.е. можем да очакваме, че то се увеличава с нарастване на скоростта, ъгъла на атака, плътността на въздуха и пр. И наистина е така, но характерът на изменението на въздушното съпротивление е съвсем различен от този на подемната сила.

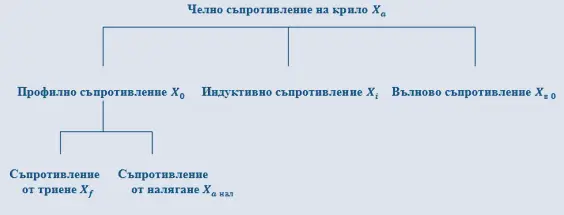
За да разберем защо обаче, първо трябва да разберем какво създава въздушното съпротивление. Оказва се, че принципно има два типа съпротивление, които допринасят за резултантната сила. Ако разгледаме по-подробно коефициента на въздушното съпротивление C_Xa от горната формула, бихме установили, че той всъщност е дефиниран като сума от два отделни съпротивителни коефициенти:

Коефициентът C_Xf  се определя от съпротивителните сили, причинени от въздушното триене, докато C_Xа нал зависи от разликата в наляганията между предната част и задната част на обтекаемото тяло.

При това съпротивлението от триене съставлява около две трети от цялото съпротивление, което изпитва един дозвуков самолет, и е определящо при по-ниски скорости.  Обаче с увеличаване на скоростта и ъгъла на атака,  трябва да сложим в сметките и съпротивлението от налягане.

Съпротивление от триене

Ключово за разбирането на съпротивлението от триене е свойството на газове и течности, наречено вискозитет. Флуидът, било то газ или течност, е съставен от множество миниатюрни молекули, които са в непрекъснато движение помежду си. Така че често се случва те да се удрят една с друга. И ако задвижим част от молекулите в дадена посока, те ще започнат да се блъскат със съседите си, придавайки им част от скоростта си и губейки част от своята. Резултатът ще е, че все повече частици ще се движат с все по-малка скорост. А за да бъде картинката максимално близка до реалността, трябва да включим и повърхността, която флуидът обтича. Тя е в твърдо агрегатно състояние – сиреч молекулите й не могат да се движат свободно. Така че когато движещи се частици от флуида се удрят в тях, те губят безвъзвратно енергията си, движението затихва и в края на краищата спира напълно.

Флуиди с различен вискозитет.

 За това колко бързо ще спре движението отговаря именно вискозитетът или по народному казано -гъстотата. Колкото по-вискозен е флуидът, толкова по-бързо престава да се движи.

Течният хелий се процежда през твърди повърхности, непроницаеми за обикновена течност. Изображение: BBC / Alfred Leitner

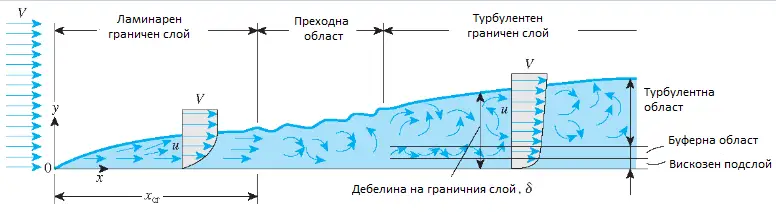
Вискозитетът на въздуха не е голям. Неговото влияние се проявява в един много тънък слой около обтекаемата повърхност на летателния апарат, наречен граничен слой. В този слой въздушните частици се „затормозяват“, скоростта им намалява, а по самата повърхност тя клони към нула, все едно че частичките са прилепнали към летателния апарат. Дебелината на граничния слой е най-малка в началото на обтичаната повърхност и нараства с отдалечаването, като най-много достига десетина милиметра.

Физически модел на течението на въздуха в граничния слой. Изображение: University of Delaware

И по-нагледна репрезентация на същото. Изображение: AllStar.fiu.edu

Течението на въздуха в граничния слой може да бъде ламинарно, турбулентно или смесено. Ламинарно течение ще рече, че частичките на въздуха се движат успоредно една на друга, без да се преместват напречно. При турбулентното течение частичките се движат хаотично, завихрено и се смесват интензивно. Смесеното течение е най-честият случай – при него граничният слой е ламинарен в началото и постепенно с увеличаване на скоростта се турбулизира, като едновременно с това увеличава и дебелината си. Пример за такова течение е димът от запалена цигара. Първоначално от нея се издига тънко стълбче пушек, който много бързо се завихря и се превръща в синкави кълба.

Като параметър за определяне на вида на граничния слой служи една от многобройните бездименсионни величини в механиката на флуидите – числото на Рейнолдс Re. Числото на Рейнолдс се дефинира като отношение на инерционните сили във флуида, отнесени към вискозните сили:

Тук 𝜌 е плътността на флуида,  V е относителната му скорост спрямо повърхността, l е характерен размер (например изминато разстояние от флуида), μ [Pa.s] е динамичен вискозитет (1.789 х 10^-5 за атмосферата на морското равнище), ν [m²/s] e кинематичен вискозитет.

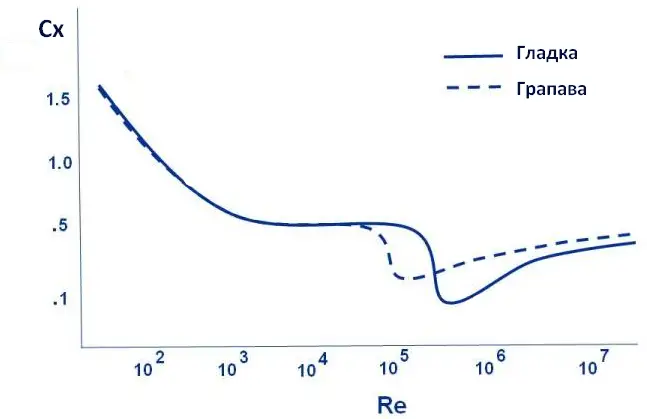
Течението e ламинарно при ниски стойности на Re, когато вискозните сили доминират. При определена стойност на Re, наречена критично число на Рейнолдс, инерционните сили са определящи и течението се турбулизира. Критичното число на Рейнолдс се определя експериментално. То зависи много от гладкостта на обтичаната повърхност (грапавините турбулизират по-бързо слоя), като в случая на плоска пластина е около 5 х 10⁵.

На тази графика е показано изменението на коефициента на съпротивление на плоска пластина в зависимост от числото на Рейнолдс. Дадени са два случая – пластина с грапава повърхност и пластина с гладка повърхност. Изображение: NASA

Както може да се очаква, вискозното триене в турбулентния граничен слой е по-голямо, отколкото в ламинарния. Затова в повечето случаи  обтекаемите повърхности се правят така, че слоят да е ламинарен, колкото се може по-дълго. Казвам в повечето случаи, защото турбулентният граничен слой има и едно важно предимство – способността му да се откъсва по-трудно от обтекаемия обект при високи скорости и ъгли на атака.

Съпротивление от разлика в наляганията

Дотук разкрихме половината от историята на въздушното съпротивление. Половината, която е малко или много интуитивна – все пак триенето е нещо, което сме свикнали да виждаме навсякъде всеки ден. Другата част от въздушното съпротивление – съпротивлението от налягане, е особеност, характерна само за протичащите флуиди.

Всички  сме чували да се говори за лошо обтекаеми или добре обтекаеми тела, но не всеки се е замислял за физическия смисъл, който се крие зад тези понятия. Нещата стоят така, че при някаква стойност на Re идва момент, при който настъпва интересно явление – граничният слой се „откъсва” от обтекаемата повърхност.

Откъсване на потока от крилен профил при надкритични ъгли на атака. Изображение: Deutsches Zentrum für Luft- und Raumfahrt

 При това тялото вече не се обтича плавно от въздуха. Ефективният му размер, дефиниран от граничния слой, се увеличава, което води и до нарастване и на триенето. Но не в това е голямата беда. Въздухът под откъснатия граничен слой се характеризира с по-малко статично налягане, отколкото има въздухът в началните участъци на обтичане, където граничният слой все още не се е откъснал. Получава се разлика в наляганията между предния и изходящия край на обтекаемото тяло, поради която се явява допълнителна сила, сякаш „бутаща“ тялото назад.

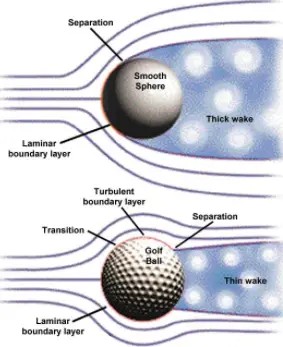
Това именно е съпротивлението от налягане. Ламинарният граничен слой е по-склонен към откъсване (защото триенето с обтекаемата повърхност е по-малко, схващате ли?) и именно поради тази причина понякога се налага въздухът в граничния слой умишлено да се турбулизира, за да се предпази от откъсване.

Потокът се откъсва по-трудно при надупчената топка за голф, отколкото при гладката, което намалява съществено въздушното й съпротивление. Изображение: Aerospaceweb.org

И следователно  така трябва да изглежда колата ви, ако искате да спестите малко гориво! Изображение: Mythbusters / Discovery Channel

Нека обобщим всичко казано до тук – въздушното съпротивление, което би изпитвало едно тяло, зависи от формата му, от гладкостта му и от параметрите на въздуха. Колкото по-тумбесто е, толкова по-лоша е картинката на обтичането му и това е причината всички летящи и плаващи апарати да се правят с удължени и плавни форми.

Индуктивно съпротивление

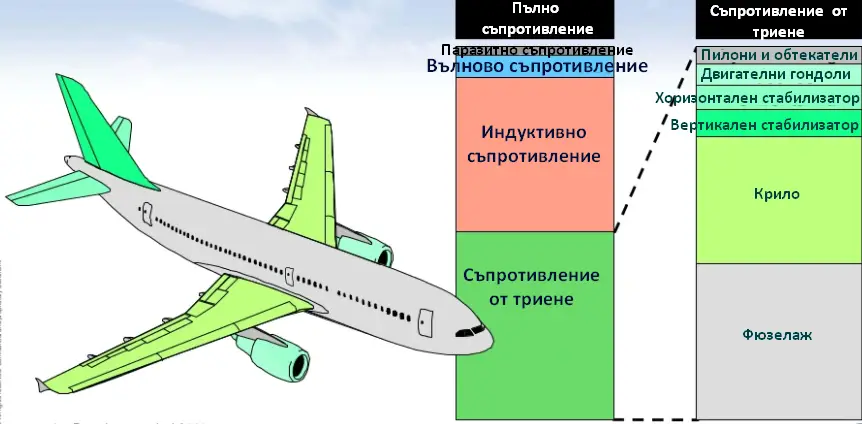
Сами разбирате, че да се направи теоретична оценка за съпротивлението (и подемната сила) на един цял летателен апарат е на практика невъзможно. Но пък е необходимо. Затова се подхожда по следния хитроумен начин – определят се съпротивленията на отделните части, от които се състои летателния апарат и след това се сумират, като се прибавя (може и да се извади, в зависимост от случая) още съпротивление от взаимното влияние на компонентите.

Дори картинката на един триизмерен обект, какъвто е крилото, е по-сложна, отколкото тази на неговия двумерен профил. На практика съпротивлението, което би имало то, е повече, отколкото ако се отчита само интегрираното по дължината му профилно съпротивление.

Обяснението е следното. За да лети самолетът, трябва налягането над горната повърхност на крилото да е по-малко, отколкото налягането отдолу. Но в двата края на крилото въздухът с високо налягане се среща с този с ниско. Така че там той безпрепятствено заобикаля крилото и отива на горната повърхност. Резултатът е, че се създават завихряния в двете краища, които се откъсват от крилото и остават като турбулентна следа на самолета в атмосферата.

Вихри, създадени от краищата на крилото на Boeing 777. Снимка: Matt Taylor.

Всичко това води до допълнително челно съпротивление, наречено индуктивно съпротивление. При малки ъгли на атака то е незначително. С увеличаване на α обаче се увеличава и разликата в наляганията между двете повърхности на крилото и индуцираното съпротивление расте.

Така че коефициентът на челно съпротивление на крилото се изразява като сума от профилното съпротивление при нулев ъгъл на атака C_X0 (което пък е сума от съпротивленията от триене и налягане, прибилизително равно на ) и индуктивно съпротивление АC_YA²  :

Както виждаме, индуктивното съпротивление зависи от коефициента на подемна сила, който е мерило за разликата между наляганията. Коефициентът на индуктивност A от своя страна зависи от  геометрията на крилото и от числото М.

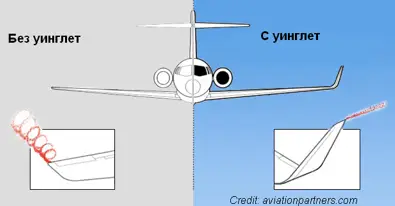Намаляване на индуктивното съпротивление посредством уинглети.

Вълново съпротивление

Остава да споменем и за още нещо. Въздухът, като всеки газ, притежава свойството свиваемост, което има доста важна роля в  аеродинамиката при високи скорости (над M = 0). Ако разглеждаме обтичането на един крилен профил с положителна кривина ще забелeжим, че скоростта, която въздухът придобива над горния контур, е по-голяма от тази на несмутения въздушен поток. В това няма нищо чудно, то е просто следствие от Закона на Бернули.

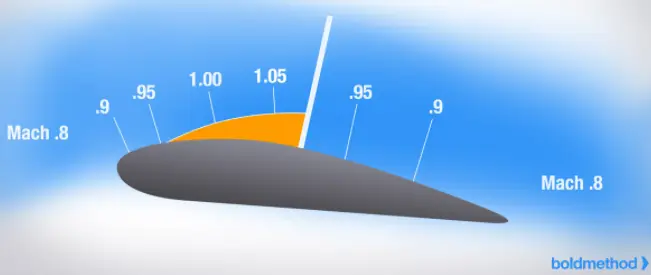
Ако обаче увеличаваме скоростта на въздушния поток, ще се стигне до момент, в който част от течението, обтичащо горната повърхност на профила, ще стане свръхзвуково. Тази скорост на несмутения поток се нарича критично число на Мах (М_кр). Оттук насетне (до достигане на М = 1) профилът ще се обтича смесено – част от него от дозвуково течение, а друга – от свръхзвуково. Свръхзвуковото течение обаче е свързано с образуването на скокове на уплътнение в предната част на профила с повишено налягане.

Скок на уплътнение върху горната повърхност на профил при скорост на обтичане над критичното число на Мах.

А това води до ново съпротивление от налягане, което се нарича вълново съпротивление (самото явление на смесено обтичане е известно като вълнови кризис). Освен че се увеличава драстично общото съпротивление на летателния апарат се получава и „бафтинг” – тресене като при достигане на критичен ъгъл на атака. Именно поради тази причина съвременните дозвукови самолети са ограничени в скоростта си до около 0.8 М, когато започва да се проявява вълновото съпротивление.  Свръхзвуковите самолети в прехода си между дозвукова и свръхзвукова скорост също гледат да съкратят максимално престоя си в диапазона между 0.8 и 1 М, където изпитват най-голямо съпротивление. А с увеличаване на скоростта вълновото съпротивление изчезва, защото целият профил започва да се обтича свръхзвуково.

Обобщение

Доста съпротивления станаха и за да няма объркване, нека ги обобщим за последно:

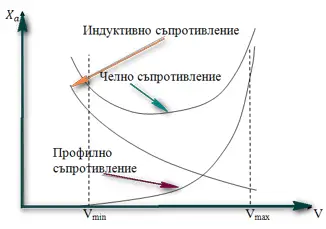
A ако се питате как се променят различните съпротивления в зависимост от скоростта на обтичане, запознайте се със следната сложна графична зависимост:

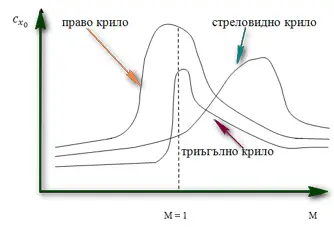
Както виждате, с увеличаване на скоростта профилното съпротивление нараства, а индуктивното намалява. Сумирайки двете съпротивления излиза, че общото челно съпротивление първоначално намалява, достига своя минимум и след това нараства. Но ако включим в играта и вълновото съпротивление, картинката се променя драматично. На долната графика виждате как, за трите най-разпространени типа крило (право, стреловидно и триъгълно):

Видно е, че развитието на вълновия кризис е по-бавно при стреловидното и тригълно крило, Те имат много по-високи стойности на  М_кр, отколкото правото крило. Освен това пикът на вълново съпротивление за стреловидното крило е изместен в свръхзвуковата област. Причината за това е, че нормалната компонента от скоростта на въздушния поток, от която всъщност зависи съпротивлението, намалява с увеличаване на ъгъла на стреловидност – т.е. самолетът може и да се движи със свръхзвукова скорост, но крилото му ще се обтича със смесен поток, ако е достатъчно стреловидно.

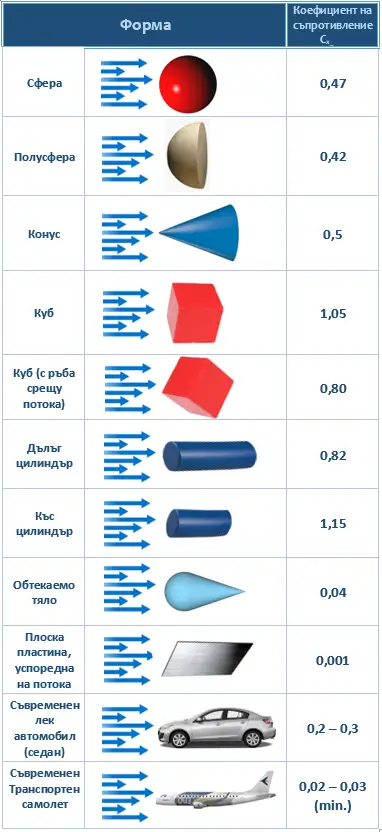
В таблицата по-долу е показан коефициентът на челно съпротивление за някои основни геометрични тела, обтичани с флуид при число на Рeйнолдс Re = 10 000.

Разпределение на основните приносители на съпротивление в самолет А-320. Изображение: Airbus

Свободно падане

Ако започнем да падаме от някаква височина, движението ни се определя от две неща – гравитационната сила и въздушното съпротивление. Без въздух скоростта, която бихме имали при такова падане, се определя просто като V = gt²/2. Или V = √(2gh),  ако я разпишем, отчитайки височината на падане. Очевидно скоростта би се увеличавала квадратично до срещането на земната твърд. И това е една добра апроксимация при падане от много малки височини. Може би спомняте онези учебникарски задачки по физика – определете дълбочината на кладенец, като хвърлите вътре камък и засечете колко време изминава, докато чуете цамбурване.

Само че наличието на въздух осезаемо променя този модел. Както видяхме по-горе, съпротивлението, което той оказва, също се изменя по квадратична зависимост с увеличаване на скоростта. Това, което реално се получава е, че падащото тяло първоначално се ускорява и в някакъв момент започва да пада с постоянна скорост, наречена гранична скорост. Тази гранична скорост зависи от площта на падащия обект в план, масата  и коефициентa му на триене, както и от плътността на въздуха, по следната формула:

Малко отклонение. Някога Аристотел твърдял, че ако пуснем две тела с различна маса, по-тежкото ще падне на земята по-бързо от по-лекото. Тази идея просъществувала непоклатима почти две хилядолетия, докато един италианец на име Галилео Галилей не решил да я провери експериментално. Легендата твърди, че той се качил на върха на наклонената кула в родния си град Пиза, от където пуснал eдно желязно гюле с маса 10 фунта и едно желязно топче с маса 1 фунт. Според Аристотел гюлето трябвало да удари земята първо, обаче за всеобщо учудване и гюлето, и топчето паднали за едно и също време. Галилей доказал, че гравитацията ускорява еднакво физическите обекти без значение от масата им.

Галилео Галилей мята железни топки от върха на наклонената кула в Пиза. Изображение: http://www.newtonsapple.org.uk

Но всъщност експериментът му не е бил достатъчно прецизен. Ако беше, той щеше да отчете, че по-тежкото гюле все пак е изпреварило с мъничко по-лекото топче. Означава ли това, че Аристотел е бил прав? Ами не. Изводите на Галилей са били съвършено верни, както доказва и сходният експеримент с чук и перо, проведен на Луната.  Но на Земята той просто не е могъл да се отърве от въздушното съпротивление.

Разглеждайки в детайли експеримента на Галилей, ще открием, че граничните скорости на гюлето и топката биха били различни. По-малката топка действително изпитва и по-малко въздушно съпротивление, но докато сметките показват, че повърхността, а следователно и въздушното съпротивление на топчето е едва 22 % от повърхността на гюлето, неговата маса е само 10 % от масата на гюлето. Кулата в Пиза е твърде ниска, за да достигнат двете гюлета граничните си скорости, но ако тя беше няколко пъти по-висока, Галилей щеше да установи, че десет фунтовото гюле  пада с  около 1,4 пъти по-висока скорост от един фунтовото. Заради въздушното съпротивление.

А каква е граничната скорост на човек и от каква височина той би я достигнал? Отговорът на тези въпроси зависи от някои допускания, които трябва да направим. Ако приемем, че човекът е заел аеродинамично най-лошата поза (с разперени крайници и лице към земята) и плътността на въздуха е константна, то сметките на база по-горната формула показват, че той би падал с около 200 km/h. Ако е заел аеродинамична поза (ръце и крака плътно прибрани, глава, насочена към земята), той може да увеличи тази скорост повече от два пъти. Рекордът се държи от Феликс Баумгартнер, който преди няколко години успя да изпревари звука при скока си от стратосферата.

Феликс Баумгартнер става свръхзвуков. Колаж от интернет.

А за да определим времето за достигане на гранична скорост, трябва да се реши следното диференциално уравнение:

Откъдето за времето t получаваме:

където V_t e граничната скорост. Kоето при достигане на 99 % от граничната скорост (V ≈ V_t) се свежда до t = 2.65*(V_t/g). Тази функция се изменя хиперболично и клони към безкрайност с доближаване на скоростта на падане V до граничната скорост V_t. Тоест граничната скорост всъщност никога не може да бъде напълно достигната!

А височината, от която трябва да скочим, за да доближим граничната скорост, може да се определи аналогично като:

За човека, разперил ръце от примера по-горе, тази височина съответства на около 600 m.  Което означава, че да скочите от сто и двайстия етаж на Бурдж Халифа е все същото като да скочите от самолет  на няколко километра височина – и в двата случая при сблъсъка си със земята бихте имали скорост от около 200 km/h.

Използвана литература:

Аеродинамика на летателните апарати, Диан Гешев, 2001, ТУ София

Още за аеродинамиката:

Динамика на полета – аеродинамични моменти

Да изпревариш звука…

Основи на аеродинамиката или защо летят самолетите

Координатни системи и сили в аеродинамиката